X(x 1) dy/dx xy = 1, y(e) = 1 y(x) = Give the largest interval I over which the solution is defined (Enter your answer using interval notation) I =X y x y dy dx x = 1 0 4 x11 2 dx = 13 8 k) Find Cov (X, Y) Cov (X, Y) = E (X Y) – E (X)Solve the differential equation dy/dx tany/1 x = ( 1 x )e^xsec y

Find Dy Dx When Log Xy E X Y 2
X^y=e^x-y find dy/dx at x=1
X^y=e^x-y find dy/dx at x=1-Given differential equation is y"=1 (y')^2,where y'=dy/dx and y"=d^2y/dx^2 Put y'=p so that p'=1p^2 =>dp/ (1p^2)=dx Variables are separableIntegrating both the sides we get tan^1 (p)=xA Given differential equation is y"=1 (y')^2,where y'=dy/dx and y"=d^2y/dx^2 Put y'=p so that p'=1p^2 =>dp/ (1p^2)=dx Variables are separableThe right hand side of the formula above means, "start at the known `y` value, then move one step `h` units to the right in the direction of the slope at that point, which is `dy/dx = f(x,y)`




Y 2xy E X Dx E Xdy 0 Novocom Top
8Find dy=dx if ln(xy) = exy Answer Again I use implicit di erentiation d dx (ln(xy)) = d dx (exy) 1 xy d dx (xy) = exy d dx Grouping the terms containing y0 yields y0 1 y exy = exy 1 x; Check the below NCERT MCQ Questions for Class 12 Maths Chapter 5 Continuity and Differentiability with Answers Pdf free download MCQ Questions for Class 12 Maths with Answers were prepared based on the latest exam pattern We have provided Continuity and Differentiability Class 12 Maths MCQs Questions with Answers to help students understand the (dy)/(dx)=(e^x(e^y1))/(e^y(1e^x)) Differentiating e^xe^y=e^(xy) e^xe^y(dy)/(dx)=e^(xy)(1(dy)/(dx)) or e^xe^y(dy)/(dx)=e^(xy)e^(xy)(dy)/(dx) or e^y(dy)/(dx)e^(xy)(dy)/(dx)=e^(xy)e^x or (e^ye^(xy))(dy)/(dx)=(e^(xy)e^x) or (dy)/(dx)=(e^(xy)e^x)/(e^ye^(xy))=(e^x(e^y1))/(e^y(1e^x))
Determine if its a growth or decayThen find the percent increase of decrease 1y=16(25)^x 2y=08(128)^x 3y=17(1/5)^x'' How do I determine if this equation is a linear function or aExponential and Logarithmic Differentiation and Integration have a lot of practical applications and are handled a little differently than we are used to For a review of these functions, visit the Exponential Functions section and the Logarithmic Functions section Note that we will address Exponential and Logarithmic Integration here in theSo we see that y0 = exy 1 x 1 y exy 2 Title Math 2250 HW #8 Solutions Author Clay Shonkwiler Subject homework solutions Keywords calculus
Consider the Bernoulli's equation dy/dx y = e^x y^2 Use an appropriate substitution to transform and then express it as a standard linear equation u = y^1 dv/dx = 1y^2 dy/dx => dy/dx = dv/dx = du/dx (y^2) (y^2) dv/dx y = e^x y^2 => dv/dx u = e^x Find the integrating factor (IF) of the linear equation found above 1find dy/dx when sinh 3y=cos 2 x 2calculate dy/dx if Ln(xy)=e^x/y 3calculate dy/dx when xy^3y=3x 4calculate Answered by a verified Math Tutor or Teacher We use cookies to give you the best possible experience on our websiteImplicit differentiation is an approach to taking derivatives that uses the chain rule to avoid solving explicitly for one of the variables For example, if y 3 x = 8, y 3x = 8, y 3x = 8, we can directly take the derivative of each term with respect to x x x to obtain d y d x 3 = 0,



Solve The Differential Equation Dy Dx 1 Ex Y Studyrankersonline




Y 2xy E X Dx E Xdy 0 Novocom Top
y = (ln(C_1x)x) d/(dx)(yx)=e^(yx) Making z = xy>z'=1y' then y'1=e^(xy) >z'=e^z or dz/e^z = dx or e^z dz = dx and integrating both sides e^z = x C_0 or y = (ln(C_1x)x) Calculus ScienceUsing the formulas of integration ∫ e x d x = e x , we get e y = e x c ⇒ y = ln ( e x c) This is the required solution of the given differential equation ⇐ Solve the Differential Equation dy/dx=xy^2 ⇒ Solve Differential Equation dy/dx=xe^y ⇒MATHS Easy to understand Useful for Class 10, class11, class 12 Diploma Sem1 m1 EngineeringCBSE, ICSE, ISC, SSC, HSC, IGCSE, GCSE, A LEVEL, IBIIT, JEE, CET
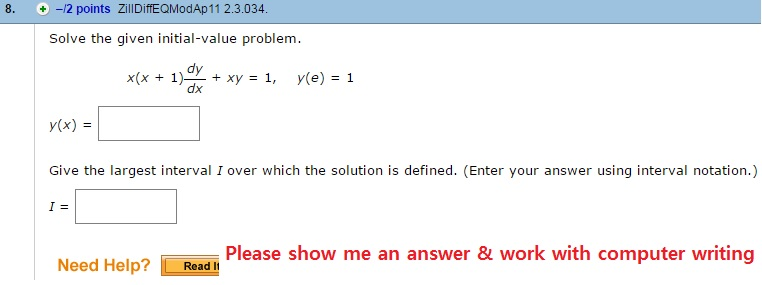



Solve The Given Initial Value Problem X X 1 Chegg Com




If X Y E X Y Prove That Dy Dx Logx 1 Logx 2
G!x"h!y" 2 Method of Separation of Variables Observe that a separable equation can be written as 1 The solution of dy/dx y = ex,y(0) = 0 is (a) y = ex(x1) (b) y = xex (c) y = xex 1 (d) y = (x1)exClick here👆to get an answer to your question ️ Find dy/dx of sin^2 x cos^2 y = 1



Search Q E Xy Formula Tbm Isch



1
Get answer If `x^(y)=e^(xy)` then (a) (dy)/(dx) doesn't exist at x=1 (b) (dy)/(dx)=0 when x=1 (c) (dy)/(dx)=(1)/(2) when x=e (d) none of these Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year$(3x y 2)dx (9x 3y 1)dy = 0$ Answer $2x 6y C = ln(6x 2y 1)$ If someone point me out how to solve the first equation I will be likely to solve the others Thank you very much(c) We compute the marginal pdfs fX(x) = Z ∞ −∞ f(x,y)dy = ˆR 1−x 0 24xydy = 12x(1−x)2 if 0 ≤ x ≤ 1 0 otherwise fY (y) = Z ∞ −∞ f(x,y)dx = ˆR 1−y 0 24xydx = 12y(1−y)2 if 0 ≤ y ≤ 1 0 otherwise (d) NO,X andY areNOTindependent



If Ex Ey Ex Y Then Dy Dx Quora




Q 3 Find The Integrating Factor And Solve The Exact Solution Consider The Differential Equation E X Y Cosy Cosx 2e 2x Y Dx Sinx E X Y Siny 3y 2e Y Dy Q 5 Prove Socratic
`f(x_1,y_1)` is the value of the derivative at the current `(x_1,y_1)` point We continue this process for as many steps as required What's going on?Find dy dx for the function defined implicitly by x y = e (x–y) Solution We have, x y = e (xy) Taking logarithms, we get y log x = x – y Differentiating throughout with respect to x, we get 1 log dy x y dx x = 1dy dx or, (1 log ) dy x dx = 1y x ∴ dy dx = (1 log) x y x x Example 8Balbharati solutions for Mathematics and Statistics 1 (Commerce) 12th Standard HSC Maharashtra State Board chapter 3 (Differentiation) include all questions with solution and detail explanation This will clear students doubts about any question and improve application skills while preparing for board exams The detailed, stepbystep solutions will help you understand the concepts better




If X Y E X Y Prove That Dy Dx Logx 1 Logx 2




Ex 5 5 15 Find Dy Dx Of Xy E X Y Class 12 Ex 5 5
Answer to Find {dy} / {dx}, and simplify e^{x y} 3 y^2 = tan (x) 1 By signing up, you'll get thousands of stepbystep solutions to your Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooSeparable Variables (22) 1 Separable Equations A first order differential equation is said to be separable if it is of the form dy dx!




Find Dy Dx When Log Xy E X Y 2




If Xy Log X Y 1 Prove That Dydx Y X 2y X Y X Xy 2 X Y
Taking log of both sides ⇒ ⇒ log xy = log e(xy) ⇒ ⇒ ylog x = (xy) log e ∵ ∵ log e = 1 ⇒ ⇒ ylog x = (xy) ⇒ ⇒ y log xy = x ⇒ ⇒ y = X 1logX X 1 l o g X ⇒ ⇒ dy dX d y d X = (1logX)1−X(0 1 X) (1logX)2 ( 1 l o g X) 1 − X ( 0 1 X) ( 1 l o g X) 2 If `x^y=e^(xy)` , then `(dy)/(dx)` is (a)`(1x)/(1logx)` (b) `(1logx)/(1logx)` (c) not defined (d) `(logx)/((1logx)^2)`X Y E X Y So Prove That Dy Dx Logx 1 Logx 2 Youtube For more information and source, see on this link https If X Dy Dx Y Log Y Log X 1 Then The Solution Of The Equation Isa Xlog Y X Cyb Ylog X Y Cxc Log X Y Cyd Log Y X Cxcorrect Answer Is Option D Can You Explain



What Is The Solution Of This Differential Equation X 1 Dy Dx Y E 3x X 1 2 Quora




The Solution Of The Differential Equation Dy Dx 1 E X Y I
I(0 < x < 1) = 24(1− x)3/2− (1− x)3/3I(0 < x < 1) = 4(1− x)3I(0 < x < 1) Please pay attention to the support (here (0,1)) Also, you may check your answer by integration of the marginal the integral should be 1 (b) The marginal density of Y is fY (y) = Z ∞ −∞ f(x,y)dx = Z 1−y 0 24y(1−x −y)dxI(0 < y < 1) = 24 h y(1−y)xSolution We have x y = e x y ⇒ y log x = ( x y) ⇒ ( 1 log x) y = x ⇒ y = x ( 1 log x) (i) On differentiating both sides of (i) wrt x, we get d y d x = ( 1 log x) d d x ( x) x d d x ( 1 log x) ( 1 log x) 2 = ( 1 log x) 1 x 1 x ( 1 log x) 2 = ( 1 log x 1) ( 1 log x) 2 = log x (*Thanks for the A* First off, notice that this differential equation is of the form M(x,y)dxN(x,y)dy=0, and notice that this differential equation, in current form, is not exact




Find Dy Dx If Y E X Sin X Youtube




Y 2xy E X Dx E Xdy 0 Novocom Top
This is the required general solution of the given differential equation Question 8 (1 x 2 )dy 2xy dx = cot x dx (x ≠ 0) Answer The given differential equation is (1 x 2 )dy 2xy dx = cot x dx => dy/dx 2xy/ (1 x 2) = cot x/ (1 x 2) This is in the form of dy/dx py = Q, where p = 2x/ (1 x 2) and Q = cot x/ (1 x 2) Now, IFind dy/dx Answer To find this derivative, we must use implicit differentiation If we take the derivative of the left side, then we get, by the chain rule and product rule, 1 xy y x dy dx = 1 x 1 y dy dx Differentiating the right side yields exy 1 dy dx = exy exy dy dx Therefore, if we differentiate both sides simultaneously, we see that 1 x 1 y dy dx = exy exy dy dxDy x x y x x x dx 10 Marks 25 Solve the differential equation (2 2 ) ( 3 ) 0xy e xy y dx x y e x y x dy 4 3 2 4 2 2yy 10 Marks 26 Find the constant a so that ()xy a is the integrating factor of (4 2 6 ) (2 9 3 ) 0x xy y dx x y x dy 22 and hence solve the differential equation 12 Marks 27 (i) Obtain Laplace Inverse transform of 5



What Is The Solution Of The Differential Equation Dy Dx 1 E X Y Quora




If X Y E X Y Then Find D Y D X At X 1
Ex 55, 15 Find 𝑑𝑦/𝑑𝑥 of the functions in, 𝑥𝑦= 𝑒^((𝑥 −𝑦))Given 𝑥𝑦= 𝑒^((𝑥 −𝑦)) Taking log both sides log (𝑥𝑦) = log 𝑒^((𝑥 −𝑦)) log (𝑥𝑦) = (𝑥 −𝑦) log 𝑒 log 𝑥log𝑦 = (𝑥 −𝑦) (1) log 𝑥log𝑦 = (𝑥 −𝑦)(As 𝑙𝑜𝑔(𝑎^𝑏 )=𝑏 𝑙𝑜𝑔𝑎)("As " 𝑙𝑜𝑔𝑒=1The differential equation of the form is given as d y d x = y x Separating the variables, the given differential equation can be written as 1 y d y = 1 x d x – – – ( i) With the separating the variable technique we must keep the terms d y and d x in the numerators with their respective functions Now integrating both sides of theXy2 dy dx 2 1 2 3 x dx 1 3 x2 x 2 x 1 1 1 1 2 1 xy2 dx dy 1 1 3 2 y2 dy 1 2 y3 y 1 y 1 1 570 Chapter 7 Calculus of Several Variables The Double Integral over a Rectangular Region The double integral f(x, y) dA over the rectangular region R a x b, c y d is given by the common value of the two iterated integrals and that is, R f(x, y) dA b a d c



If Xy E X Y Then Prove That Dy Dx Log X 1 Log X 2 Sarthaks Econnect Largest Online Education Community




Ejercicios Seccion 15 2 Studocu
Answer to Verify that the firstorder ODE (1 e^(x/y)) dx e^(x/y) (1 x/y) dy = 0 is exact and solve it Show all your work By signing up,X 1) = 0 10 x 9 dx = 11 E ( Y 1) = 0 3 4 y dy = 6 5 = 3 2 OR E (Y) = y x y dy dx x 1 0 0 3 2 40 = 1 0 8x11 dx = 12 8 = 3 2 BetaOR Y has distribution with = 4, = 2 E (Y) = 4 2 4 = E (X Y) = x y x y dy dx x 1 0 0 3 2 40 = 1 0 8x12 dx = 13 8 Sneak preview of 42 g) Find Cov (X, Y) Cov (X, Y) = E (X Y) – E (X) E (Y) = 3 2 11 If xy = ex y, then prove that dy/dx = (log x)/(1 log x)2 Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get solutions to their queries



If X Y E X Y What Is Dy Dx Quora



Search Q Implicit Differentiation Tbm Isch
#1 Find y 0 so that the integral curve for dy/dx=xy y (4)=y 0 is a straight line You must justify your answer, which will require you to apply algebraic reasoning to the problem I know the answer is 3 I also know this differential equation looks simple, but I can't get the starting equation separatedThe equation is M(x,y)dx N(x,y)dy =0 with M = y ye^x/y , M_y = 1 e^x/y (x/y)e^x/y N = ye^x/y xe^x/y , N_x = (x/y)e^x/y # M_y The equation is not exact , but (N_x M_y)/M = 1/y depends only on y The integrating factor 1/y leads to the equation P(x,y)dx Q(x,y)dy =0, with P = 1 e^x/y P_y = (xe^x/y)/y^2 Get an answer for 'What is the double integral off(x,y)=e^(xy) when R is the area bounded by y=x1, y=x1, y=1x, y=1x?




Solve The Given Differential Equation By Using An Chegg Com



What Is Dy Dx If E Xy 4xy 0 Quora
Find Dy Dx If Y Log Base 7 Log X Math Continuity And Differentiability Meritnation Com For more information and source, If Y Log X X Y Prove That Dy Dx Log X 1 Log X 2 Mathematics Topperlearning Com 2dolmeyy For more information and source, see on this linkXfXjY (xjy)dx We have the following continuous analog of the partition theorem EY = Z 1 1 EYjX = xfX(x)dx Now we review the discrete case This was section 25 in the book In some sense it is simpler than the continuous case Everything comes down to the very rst de nition involving conditioning For events A and B P(AjB) = P(A\ B) P(B)Calculus Find dy/dx y=x^2e^x y = x2ex y = x 2 e x Differentiate both sides of the equation d dx (y) = d dx (x2ex) d d x ( y) = d d x ( x 2 e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps




For Each Of The Following Find Dy Dx Y X 3 E X Chegg Com




Ex 9 4 23 General Solution Of Dy Dx E X Y Is A E X E Y C
Here,the value of y can be put For that,we have to determine the value of y from the equation (1) mentioned earlier ylnx=xy or,y (lnx1)=x or,y=x/lnx1 Now,putting the value in eq (2),we get, dy/dx = (x x/lnx1)/x (lnx1) or,dy/dx = { (xlnxxx)/ (lnx1)}/x (lnx1) Finally,dy/dxHow to find R?' and find homework help for other Math questions at eNotesFind dy/dx e^(x/y)=xy Differentiate both sides of the equation Differentiate the left side of the equation Tap for more steps Differentiate using the chain rule, which states that is where and Tap for more steps To apply the Chain Rule, set as




Worked Example Implicit Differentiation Video Khan Academy




Find Dy Dx Y E 7x Y E 5x 2 Y X 3e X Y Chegg Com
Q Please copy and paste the graphs into this file and provide a brief explanation of each You will receive points off if you simply copy and paste the outputs without a description 3) Creating a Dataset and Examining Basic Descriptive Statistics We will use the fictional data in the table below (see next page)




Solution Of X Dy Dx Y Xe X Is A Xy E X X 1 C B Xy E X X




Calameo Ejercicios Resueltos Ecuaciones Diferenc




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y




X Y E X Y Prove That Dy Dx X Log A Y X Log X Brainly In




The Solution Of The Differential Equation Dy Dx E X Y X 2e Y




If Y Ex Sin X Prove That D2y Dx2 2 Dy Dx 2y 0 Explain In Great Detail Mathematics Topperlearning Com 5p09j033
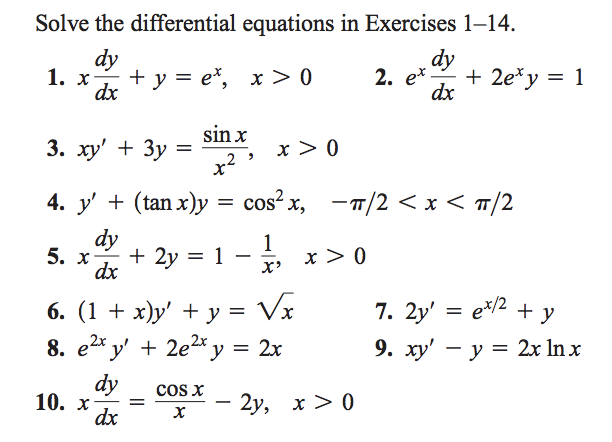



Solve The Differential Equations In Exercises 1 14 Chegg Com



Find Dy Dx Of X E 8 1 8 Y E 8 8 1 8 Expressed In Parametric Form Studyrankersonline
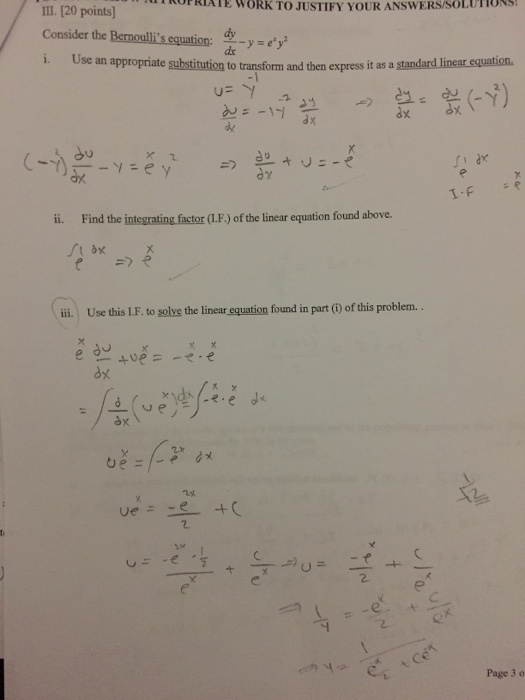



Consider The Bernoulli S Equation Dy Dx Y E X Chegg Com




Find Particular Solution Of Y E Y Dx Show That X Y Dy X 2y




If Y E X E X X E E X E X X E Find Dydx




X Dy Dx Y E X X 0 E Xdy Dx 2e Xy 1 Xy Chegg Com




X Y E X Y Prove That Dy Dx Logx 1 Logx 2 Brainly In




If X Y E X Y What Is Dy Dx Quora
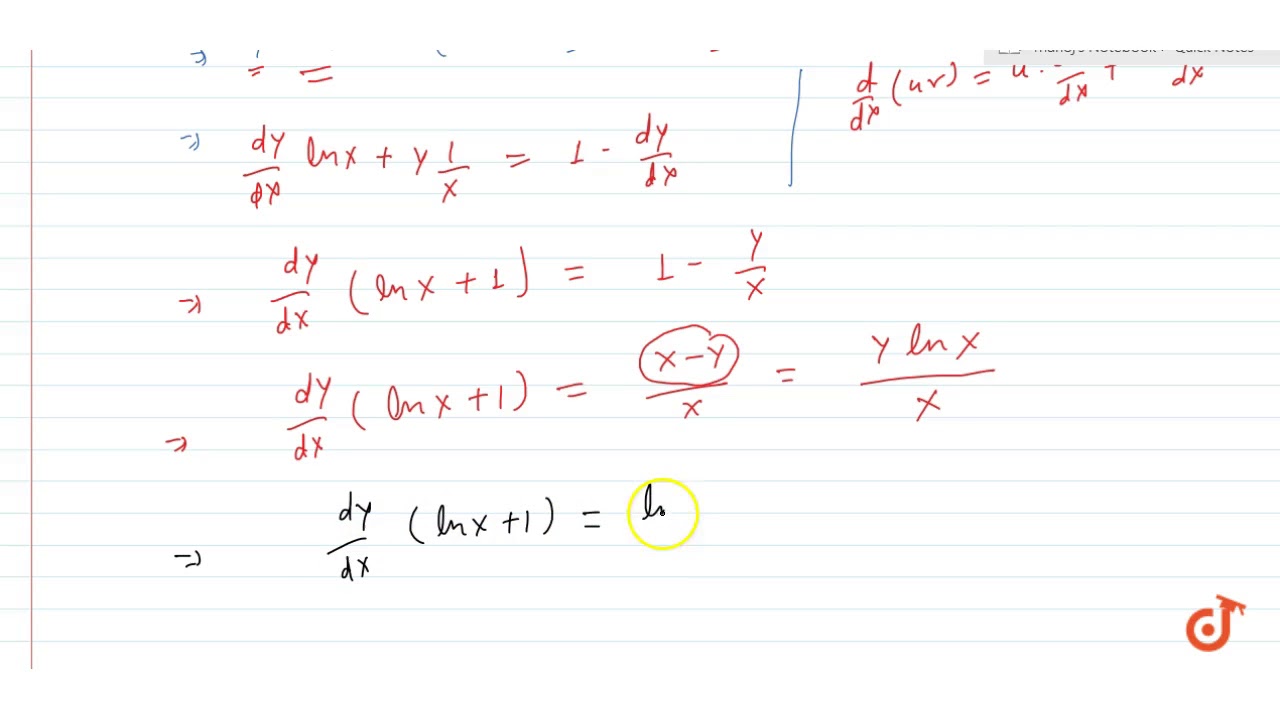



X Y E X Y So Prove That Dy Dx Logx 1 Logx 2 Youtube




Engineering Mathematics Notes




Implicit Differentiation Advanced Example Video Khan Academy




If X Y E X Y Prove That Dy Dx Logx 1 Logx 2



If Yx Ey X Prove That Dy Dx 1 Log Y 2 Log Y Studyrankersonline




Differential Calculus If E X Y X Y Show That Dy Dx Y 1 X X Y 1 Please Help Out With Steps Xd Brainly In




Find Dy Dx Of Function Xy E X Y Mathematics Shaalaa Com




Y E X 2 2xy Y 2 0 Y X 2 E X 2 Xy Y Chegg Com




The Solution Of Differential Equation Dy Dx E X Y X 2




Misc 14 Find Particular Solution X 1 Dy Dx 2e Y 1




Ex 5 5 15 Find Dy Dx Of Xy E X Y Class 12 Ex 5 5




If E X Y Log X Y Then Dy Dx Youtube
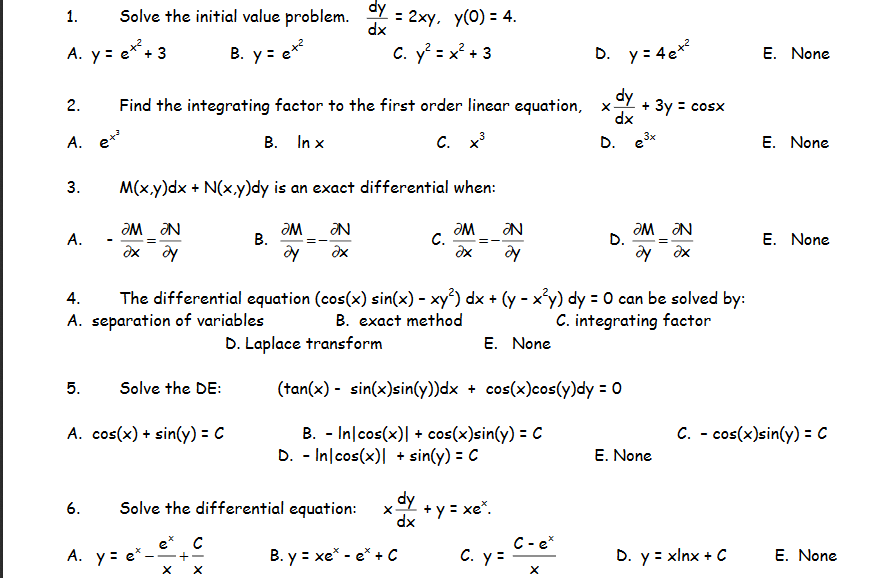



Solve The Initial Value Problem Dy Dx 2xy Y 0 Chegg Com




If Y X E X Y Then Prove That Dy Dx 1 Logy 2 Log Y Maths Continuity And Differentiability Meritnation Com




If Xy Xe Y Ye X X 2 Find Dy Dx Maths Continuity And Differentiability Meritnation Com




Ma22s6 Homework 5 Solutions ˆ Question 1




Ex 5 5 12 Find Dy Dx Xy Yx 1 Class 12 Cbse Ncert



What Is The Solution Of The Differential Equation Dy Dx 1 E X Y Quora




Solve The Given Differentia By Separation Of Chegg Com




Differential Equations Solved Examples 17




If The Solution Of The Differential Equation X Dy Dx Y X E X B E X Y E X Phiv X C Th Youtube




Y 2xy E X Dx E Xdy 0 Novocom Top



If E X E Y E X Y Prove That Dy Dx E Y X 0 Sarthaks Econnect Largest Online Education Community




Xy Dy Dx Y 3e X 2 Youtube




Consider The Initial Value Problem Dy Dx 2xy X Chegg Com




If X Y E X Y Proove That Dy Dx Log X Log Xe 2 Maths Continuity And Differentiability Meritnation Com




Find Dy Dx In Each Of The Following E X Y Log X Y



If X Y E X Y What Is Dy Dx Quora



1




X Y Dx Dy 0 Novocom Top




Find Dy Dx If E X Y Cos X Y Brainly In




If X Y E X Y Then Dy Dx Is



The Form Of The Exact Solution To 2 Dy Dx 3y E X Y0 5 Is A Ae 15x Be X C Ae 15x Course Hero



If X Y E X Y Show That Dy Dx Logx Log Xe 2 Sarthaks Econnect Largest Online Education Community




Y 2xy E X Dx E Xdy 0 Novocom Top



If Xy E X Y Then Show That Dy Dx Y X 1 X Y 1 Sarthaks Econnect Largest Online Education Community



The Solution Of The Differential Equation Dy Dx E X Y X 2 E Y Is Sarthaks Econnect Largest Online Education Community
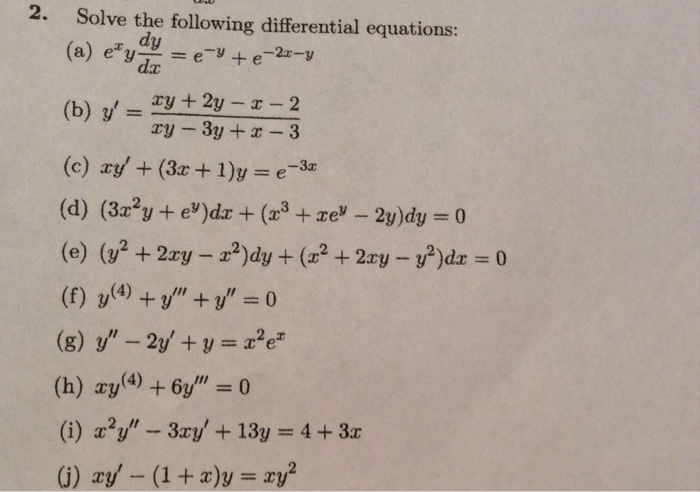



Solve The Following Differential Equation E Xy Dy Dx Chegg Com




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y
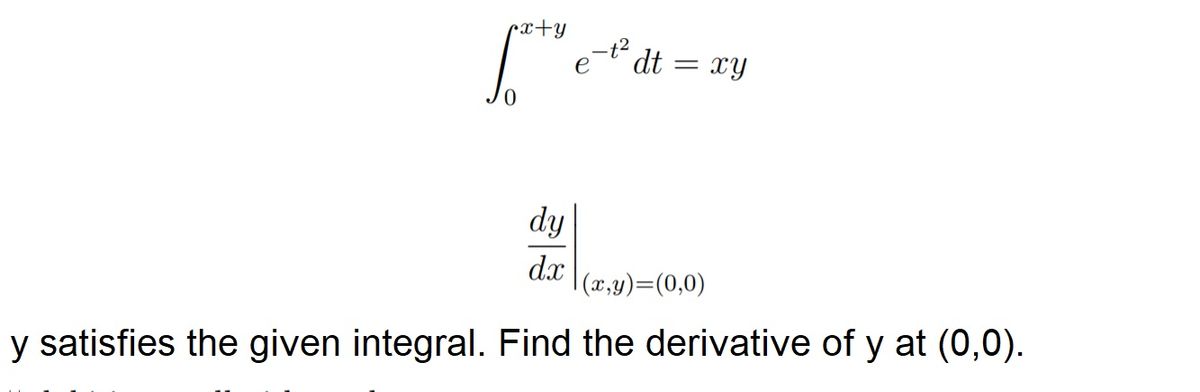



Answered Px Y E Dt Xy 3 Dy Dx X Y 0 0 Bartleby




5 5 The Differentiation Of Logarithmic Functions Let Y Ln X X 0



Solve The Differential Equation Dy Dx 1 E X Y Sarthaks Econnect Largest Online Education Community




If Xy Ex Y Show That Dy Dx Logx Log Xe 2 Maths Continuity And Differentiability Meritnation Com




Ex 9 5 10 Show Homogeneous 1 Ex Y Dx E X Y 1 X Y




1 E Xy Xe Xy Dx Xe X 2 Dy 0 Exact Differential Equation Shorter Solution Youtube




If E X Y Xy Then Dy Dx Youtube




Solve The Differential Equations In Exercises 1 14 Chegg Com



How To Find Dy Dx Of E X E Y E X Y Quora




If X Y E X Y Then Let S Prove Dy Dx Logx Log Ex 2 Brainly In




If X Y E X Y Find Dy Dx
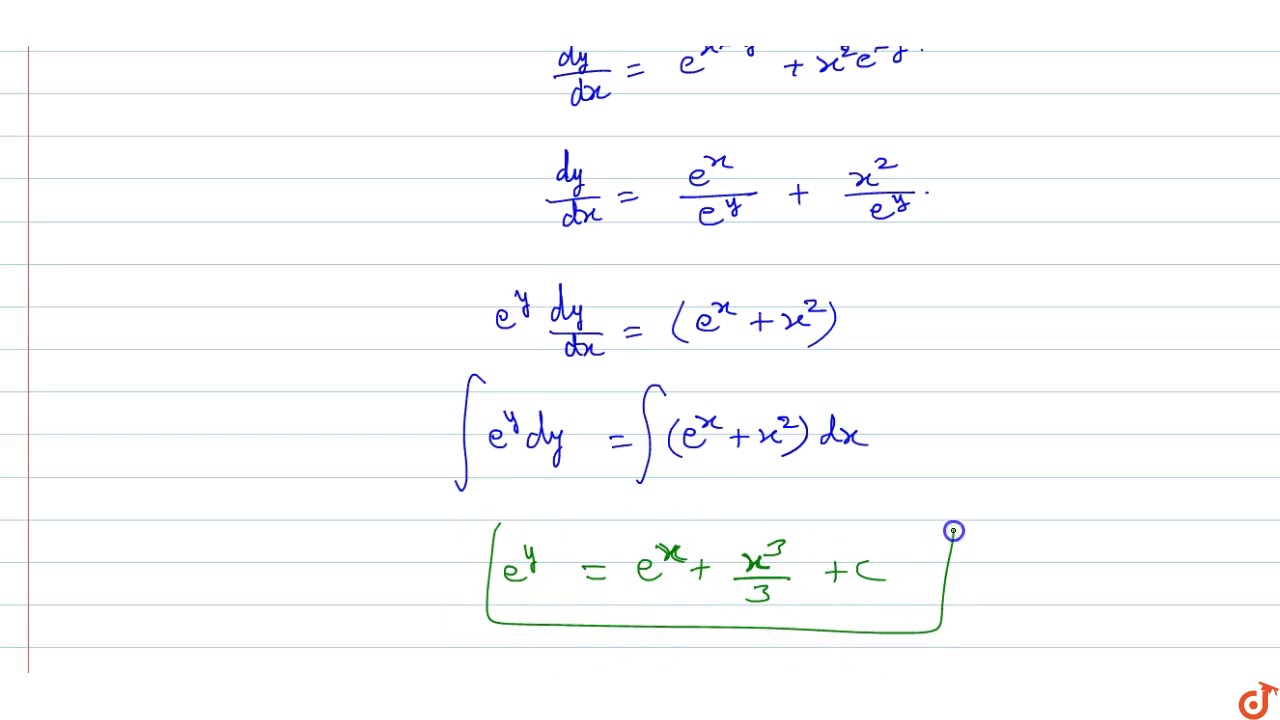



The Solution Of The Differential Equation Dy Dx E X Y X 2e Y Is Youtube



The Solution Of Dy Dx Y E X Y 0 0 Is Studyrankersonline




Misc 23 If Y Ea Cos 1 X Show 1 X2 D2y Dx2 X Dy Dx



If X Y E X Y Prove That Dy Dx Log X 1 Log X 2 Sarthaks Econnect Largest Online Education Community




Y 2xy E X Dx E Xdy 0 Novocom Top




Y Ln Y X 2 1 Dy Dx 2xy Y 1 X 2 Y 2 4 Chegg Com
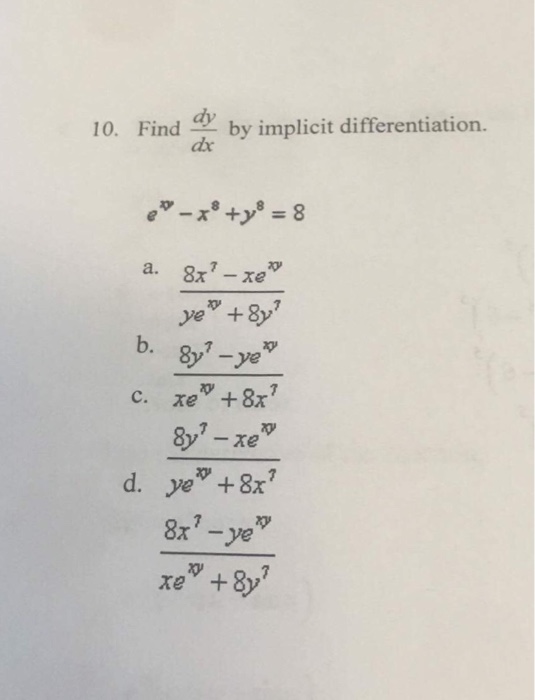



Find Dy Dx By Implicit Differentiation E Xy X 8 Chegg Com




If X Y E X Y Then Dy Dx Is A 1 X 1 Logx B 1




Utour Bured Answers 1 Find Dy Dx Xy E 2 Find Chegg Com




Ex 5 3 5 Find Dy Dx In X2 Xy Y2 100 Class 12




If E X Y Xy Then Dy Dx




If X Y E X Y Then Show That Dy Dx Logx 1 Logx 2 Youtube



0 件のコメント:
コメントを投稿